Anillo conmutativo unitario
Mira otros diccionarios:
Anillo conmutativo — Saltar a navegación, búsqueda En teoría de anillos (una rama del álgebra abstracta), un anillo conmutativo es un anillo (R, +, ·) en el que la operación de multiplicación · es conmutativa; es decir, si para cualesquiera a, b ∈ R, a·b = b·a. Si… … Wikipedia Español
Anillo conmutativo — Un anillo (no necesariamente unitario) se denomina anillo conmutativo si la operación producto ( ) cumple la propiedad conmutativa, esto es, si se cumple que cualesquiera que sean . Por lo tanto, en un anillo conmutativo, el centro del anillo… … Enciclopedia Universal
Anillo de fracciones — Saltar a navegación, búsqueda En Álgebra conmutativa son interesantes a menudo los anillo de fracciones que constituyen una generalización del concepto de cuerpo de fracciones. Construcción del anillo de fracciones de un anillo Sea un anillo… … Wikipedia Español
Anillo (matemática) — En álgebra, un anillo es una estructura algebraica formada por un conjunto (A), y dos operaciones: suma y producto; de modo que (A,+) es un grupo conmutativo con elemento neutro (que designamos 0), y el producto es asociativo y tiene la propiedad … Wikipedia Español
Anillo unitario — Saltar a navegación, búsqueda Un anillo (no necesariamente conmutativo) es anillo unitario, o anillo unital, o anillo con unidad si existe un elemento en R, diferente del neutro para la suma, que es elemento neutro para la operación producto ( ·… … Wikipedia Español
Anillo de división — Saltar a navegación, búsqueda Un anillo de división, o cuerpo torcido, o cuerpo skew, o cuerpo no conmutativo, es un anillo unitario de manera que todo elemento es invertible, es decir, si R es el anillo unitario y U(R) representa a los elementos … Wikipedia Español
Anillo de división — Un anillo de división, o cuerpo torcido, o cuerpo skew, o cuerpo no conmutativo, es un anillo unitario de manera que todo elemento es invertible, es decir, si R es el anillo unitario y U(R) representa a los elementos invertibles del anillo, .… … Enciclopedia Universal
Anillo unitario — Un anillo (no necesariamente conmutativo)es anillo unitario, o anillo unital, o anillo con unidad si existe un elemento en que es elemento neutro para la operación producto ( · ) del anillo, razón por la cual a dicho elemento se le denomina… … Enciclopedia Universal
Ideal (teoría de anillos) — En matemáticas, un ideal es una estructura algebraica definida en un anillo. Los ideales generalizan de manera fecunda el estudio de la divisibilidad en los números enteros. De este modo, es posible enunciar versiones muy generales de teoremas… … Wikipedia Español
Dominio (álgebra) — Saltar a navegación, búsqueda En Álgebra la palabra dominio presenta una seria dificultad. Por un lado designa originalmente a aquellos anillos conmutativos y unitarios en los que el elemento neutro para la suma y el elemento neutro para el… … Wikipedia Español
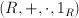es anillo conmutativo unitario si 
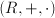es anillo conmutativo y además 
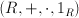es anillo unitario.
Los anillos conmutativos y unitarios son de enorme inportancia en Álgebra, particularmente en Álgebra Conmutativa y en Geometría Algebraica. A ellos son aplicables todas las propiedades tanto de anillos unitarios como de anillos conmutativos.
Los anillos conmutativos y unitarios en los que el neutro de la suma y el neutro del producto no coinciden (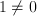
) se denominan dominios. Un dominio es pues cualquier anillo conmutativo y unitario distinto del anillo trivial 0.